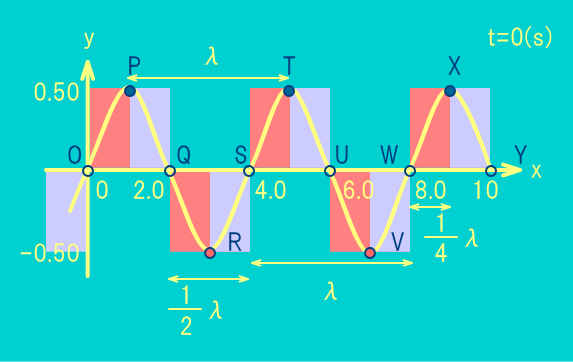
上図のように波が観察できる時,(単位はcm)
波長は(,ギリシャ文字)で表され,
8.0-4.0=.cm
この波が右方向(xの正の方向)に速さ1.0cm/sで
移動しているとすると
速さ,波長λ,振動数の間には
=λ
の関係があることが分かっている.
波を学ぶ時,一番事な式で,困ったらこの式に数値をあてはめると必要な値が出てくる.
では,振動数を求めてみよう.
=1.0cm/s,=4.0cmより
1.0=×4.0
|
|
|
|
| f= |
———— |
=0.(z) |
|
|
|
|
|
|
|
|
|
振動数は1秒間に何波長,通過するかを意味する.
逆に周期は1波長が通過するのに何秒かかるかを意味しており,
|
|
|
|
| = |
———— |
|
|
|
f |
|
|
|
|
|
|
の関係がある.つまり逆数になっている.
|
|
|
|
| T= |
———— |
=.(s) |
|
|
|
|
|
|
|
|
|
振幅は上図だと上下の振れを示しており,
振幅=0.0cmである.
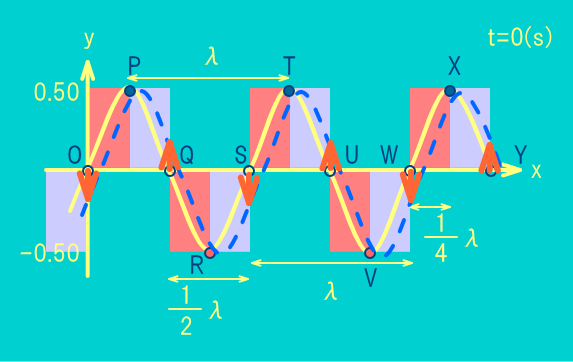
今度は各点での上下移動の速度を考える.
点Pや点Rのようなや谷の点では,上がり切ってこれから下がったり,下がり切ってこれから上がる点であるので
上下方向の速度はcm/sである.
速度0の点は
山の点P,,Xおよび
の点,Vである.
速度が最大の点は軸との交点になるので
点O,Q,,U,W,Yである.
波は右方向に移動しているので少し右にずらした波を図の青色の破線のように描くと
点Oはにずれることがわかる.
よって点Oは向きの速度が最大である.
一方,点Qはにずれることがわかる.
よって点Qは向きの速度が最大である.
このようにすると
上方向の速度が最大の点は
点Q,U,である.
下方向の速度が最大の点は
点O,,Wである.
上下の矢印をつけるときは
元の線のx軸上の点から移動した線のほうに引く.
最後にこのようなグラフはある時点での原点から各距離での位(上下方向の位置)を示しており,y-グラフと呼ぶ.
