グラフの形を見て二次関数y=ax2+bx+cの
係数等の大きさを考える問題を解いてみる.
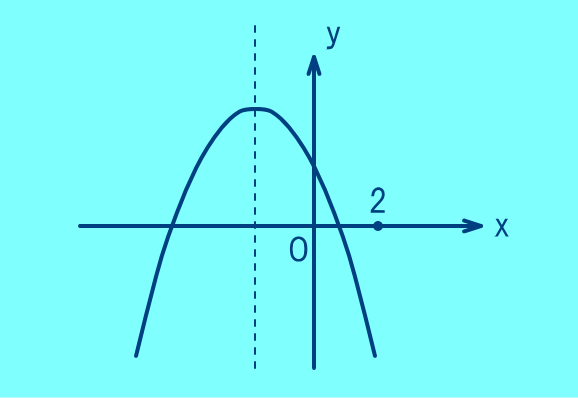
上のグラフはに凸だからa0・・・①
次にcはy片(y軸との交点)よりc0・・・②
これはx=を代入してもよい.
また,x軸(y=)との交点が2つあるので
ax2+bx+c=0で考えて
別式D=b2-4ac0・・・③
bは結構めんどい.
式を方完成して
|
|
|
2- |
b2 |
|
| y=a(x+ |
————— |
) |
——— |
+c |
|
a |
|
|
4a |
|
|
|
|
|
|
|
|
|
|
|
これより
|
|
|
|
| 軸x= |
————— |
|
|
|
a |
|
|
|
|
|
|
であることがわかる.
上図で軸は点線で表しているが,y軸より左側なので
|
b |
|
|
| 軸x=- |
——— |
0 |
|
|
2a |
|
|
|
|
|
|
①よりa<0から
b0なら分子は--でになるので不等式が成り立つ.
よってb0・・・④
y=(x)とおくと(この形は何をxに代入したか分かりやすいのでよく使う)
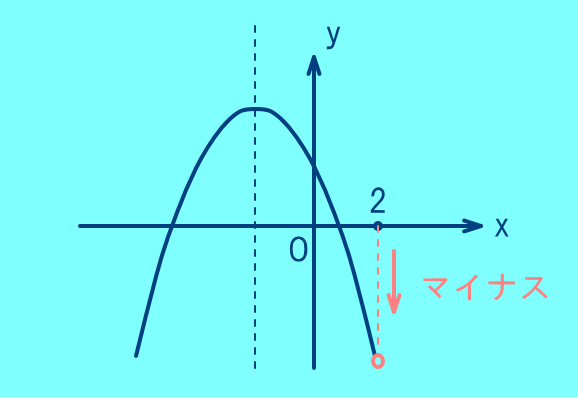
グラフのx=2のところに注目して
f()=a×2+b×+c
=a+b+c0・・・⑤であることもわかる.
これはx=のところでグラフの値がx軸より下の
マイナスであることを示している.